วิธีจับคู่ตัวเลขกับกราฟของฟังก์ชัน กราฟและคุณสมบัติพื้นฐานของฟังก์ชันเบื้องต้น ฟังก์ชันยกกำลังที่มีเลขชี้กำลังจริงที่ไม่ใช่จำนวนเต็มซึ่งมีค่าน้อยกว่าลบหนึ่ง
ฟังก์ชั่นพลังงาน
นี่คือฟังก์ชัน:
y = ขวาน n, ที่ไหน หนึ่ง- ถาวร. ที่
n= 1 เราได้ สัดส่วนโดยตรง:
ย
=
ขวาน- ที่ n
= 2 - พาราโบลาสี่เหลี่ยม
- ที่ n
=
-
1
- สัดส่วนผกผันหรือ อติพจน์.
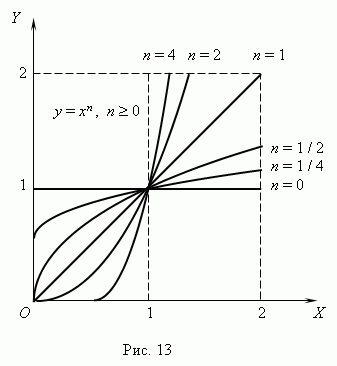
ดังนั้นฟังก์ชันเหล่านี้จึงเป็นกรณีพิเศษของฟังก์ชันกำลัง เรารู้ว่ากำลัง 0 ของจำนวนที่ไม่ใช่ศูนย์ใดๆ ก็คือ 1 ดังนั้น ณ n= 0 ฟังก์ชันกำลังจะกลายเป็นค่าคงที่:ย
=
ก, เช่น. ตารางงานของเธอคือ เส้นตรงขนานกับแกนเอ็กซ์ไม่รวมแหล่งกำเนิด (กรุณาอธิบายทำไม ? - กรณีทั้งหมดนี้ (ด้วย ก=
1
)
แสดงในรูปที่ 13
(n 0) และรูปที่ 14 ( n
< 0). Отрицательные значения
xไม่ได้รับการพิจารณาในที่นี้ดังนั้น
ชอบฟังก์ชั่นบางอย่าง:
ถ้า n– จำนวนเต็ม ฟังก์ชันยกกำลังสมเหตุสมผลแม้เมื่อใดx< 0, но их графики имеют различный вид в зависимости от того, является ли nเลขคู่หรือเลขคี่รูปที่ 15 แสดงฟังก์ชันกำลังสองฟังก์ชันดังกล่าว: nสำหรับ n = 3.
= 2 และ n= ที่2 ฟังก์ชันเป็นเลขคู่และกราฟของมันมีความสมมาตร สัมพันธ์กับแกน. ย nที่ = 3 ฟังก์ชันเป็นเลขคี่และกราฟมีความสมมาตรสัมพันธ์กับจุดกำเนิดย = x 3 พิกัด การทำงาน เรียกว่า.
ลูกบาศก์พาราโบลา รูปที่ 16 แสดงฟังก์ชัน นี้ ย = x 2 ฟังก์ชั่นคือ. ผกผันกับพาราโบลาสี่เหลี่ยม
กราฟของมันได้มาโดยการหมุนกราฟของพาราโบลาสี่เหลี่ยมรอบเส้นแบ่งครึ่งของมุมพิกัดที่ 1 นี่คือวิธีการรับกราฟของฟังก์ชันผกผันใดๆ จากกราฟของฟังก์ชันดั้งเดิม จากกราฟเราเห็นได้ว่านี่คือฟังก์ชันสองค่า (ซึ่งระบุด้วยเครื่องหมาย ± หน้ารากที่สองด้วย) ฟังก์ชันดังกล่าวไม่ได้รับการศึกษาในคณิตศาสตร์ระดับประถมศึกษา ดังนั้นในฐานะฟังก์ชันเราจึงมักจะพิจารณาสาขาใดสาขาหนึ่ง: บนหรือล่างความรู้
ฟังก์ชันเบื้องต้นเบื้องต้น คุณสมบัติ และกราฟ สำคัญไม่น้อยไปกว่าการรู้ตารางสูตรคูณ พวกเขาเป็นเหมือนรากฐาน ทุกสิ่งทุกอย่างขึ้นอยู่กับพวกเขา ทุกสิ่งทุกอย่างถูกสร้างขึ้นจากพวกเขา และทุกสิ่งทุกอย่างก็ขึ้นอยู่กับพวกเขาในบทความนี้ เราจะแสดงรายการฟังก์ชันพื้นฐานหลักๆ ทั้งหมด จัดทำกราฟ และให้ข้อมูลโดยไม่มีข้อสรุปหรือข้อพิสูจน์
- คุณสมบัติของฟังก์ชันพื้นฐานเบื้องต้น
- ตามโครงการ:
- พฤติกรรมของฟังก์ชันที่ขอบเขตของขอบเขตของคำจำกัดความ เส้นกำกับแนวตั้ง (หากจำเป็น ดูการจำแนกประเภทบทความเกี่ยวกับจุดไม่ต่อเนื่องของฟังก์ชัน)
- เส้นกำกับเฉียงและแนวนอน
- จุดเอกพจน์ของฟังก์ชัน
- คุณสมบัติพิเศษของฟังก์ชันบางอย่าง (เช่น คาบบวกที่น้อยที่สุดของฟังก์ชันตรีโกณมิติ)
หากคุณสนใจหรือไปที่ส่วนต่างๆ ของทฤษฎีเหล่านี้ได้
ฟังก์ชันพื้นฐานเบื้องต้นคือ: ฟังก์ชันคงที่ (ค่าคงที่), รากที่ n, ฟังก์ชันยกกำลัง, เลขชี้กำลัง, ฟังก์ชันลอการิทึม, ฟังก์ชันตรีโกณมิติและฟังก์ชันตรีโกณมิติผกผัน
การนำทางหน้า
ฟังก์ชั่นถาวร
ฟังก์ชันคงที่ถูกกำหนดให้กับเซตของจำนวนจริงทั้งหมดด้วยสูตร โดยที่ C คือจำนวนจริงบางตัว ฟังก์ชันคงที่เชื่อมโยงค่าจริงแต่ละค่าของตัวแปรอิสระ x กับค่าเดียวกันของตัวแปรตาม y - ค่า C ฟังก์ชันค่าคงที่เรียกอีกอย่างว่าค่าคงที่
กราฟของฟังก์ชันคงที่เป็นเส้นตรงขนานกับแกน x และผ่านจุดที่มีพิกัด (0,C) ตัวอย่างเช่น ลองแสดงกราฟของฟังก์ชันคงที่ y=5, y=-2 และซึ่งในรูปด้านล่างสอดคล้องกับเส้นสีดำ สีแดง และสีน้ำเงิน ตามลำดับ
คุณสมบัติของฟังก์ชันคงที่
- โดเมน: เซตของจำนวนจริงทั้งหมด
- ฟังก์ชันคงที่คือเลขคู่
- ช่วงของค่า: ชุดที่ประกอบด้วยตัวเลขเอกพจน์ C
- ฟังก์ชันคงที่จะไม่เพิ่มขึ้นและไม่ลดลง (เพราะเหตุนี้จึงเป็นค่าคงที่)
- มันไม่สมเหตุสมผลเลยที่จะพูดถึงความนูนและความเว้าของค่าคงที่
- ไม่มีเส้นกำกับ
- ฟังก์ชันส่งผ่านจุด (0,C) ของระนาบพิกัด
รากของระดับที่ n
ลองพิจารณาฟังก์ชันพื้นฐานพื้นฐาน ซึ่งได้จากสูตร โดยที่ n คือจำนวนธรรมชาติที่มากกว่า 1
รากของดีกรีที่ n, n เป็นเลขคู่
เริ่มต้นด้วยฟังก์ชันรูทที่ n สำหรับค่าคู่ของเลขชี้กำลังรูท n
ดังตัวอย่าง นี่คือรูปภาพที่มีรูปภาพของกราฟฟังก์ชัน 
และสอดคล้องกับเส้นสีดำ สีแดง และสีน้ำเงิน
กราฟของฟังก์ชันรูทระดับคู่จะมีลักษณะคล้ายกันกับค่าอื่นของเลขชี้กำลัง
คุณสมบัติของฟังก์ชันรูทที่ n สำหรับเลขคู่
รากที่ n คือเลขคี่
ฟังก์ชันรูทที่ n ที่มีเลขชี้กำลังรูตคี่ n ถูกกำหนดไว้บนชุดของจำนวนจริงทั้งชุด ตัวอย่างเช่น นี่คือกราฟฟังก์ชัน 
และสอดคล้องกับเส้นโค้งสีดำ สีแดง และสีน้ำเงิน
สำหรับค่าคี่อื่นๆ ของเลขชี้กำลังราก กราฟฟังก์ชันจะมีลักษณะคล้ายกัน
คุณสมบัติของฟังก์ชันรากที่ n สำหรับเลขคี่ n
ฟังก์ชั่นพลังงาน
ฟังก์ชันกำลังถูกกำหนดโดยสูตรของแบบฟอร์ม
ลองพิจารณารูปแบบของกราฟของฟังก์ชันกำลังและคุณสมบัติของฟังก์ชันกำลัง ขึ้นอยู่กับค่าของเลขชี้กำลัง
เริ่มต้นด้วยฟังก์ชันกำลังด้วยเลขชี้กำลังจำนวนเต็ม a ในกรณีนี้ ประเภทของกราฟของฟังก์ชันยกกำลังและคุณสมบัติของฟังก์ชันจะขึ้นอยู่กับความสม่ำเสมอหรือความคี่ของเลขชี้กำลัง รวมถึงเครื่องหมายด้วย ดังนั้นก่อนอื่นเราจะพิจารณาฟังก์ชันกำลังสำหรับค่าบวกคี่ของเลขชี้กำลัง a จากนั้นสำหรับเลขชี้กำลังบวกคู่จากนั้นสำหรับเลขชี้กำลังลบเลขคี่และสุดท้ายสำหรับค่าลบคู่ a
คุณสมบัติของฟังก์ชันกำลังที่มีเลขชี้กำลังที่เป็นเศษส่วนและไม่ลงตัว (รวมถึงประเภทของกราฟของฟังก์ชันกำลังดังกล่าว) ขึ้นอยู่กับค่าของเลขชี้กำลัง a เราจะพิจารณาพวกมัน ประการแรก สำหรับ a จากศูนย์ถึงหนึ่ง อย่างที่สอง สำหรับค่าที่มากกว่าหนึ่ง ประการที่สาม สำหรับ a จากลบหนึ่งถึงศูนย์ ประการที่สี่ สำหรับค่าน้อยกว่าลบหนึ่ง
ในตอนท้ายของส่วนนี้ เพื่อความสมบูรณ์ เราจะอธิบายฟังก์ชันกำลังที่มีเลขชี้กำลังเป็นศูนย์
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังบวกเป็นเลขคี่
ลองพิจารณาฟังก์ชันยกกำลังที่มีเลขชี้กำลังบวกเป็นคี่ ซึ่งก็คือ โดยมี a = 1,3,5,....
รูปด้านล่างแสดงกราฟของฟังก์ชันกำลัง – เส้นสีดำ – เส้นสีน้ำเงิน – เส้นสีแดง – เส้นสีเขียว สำหรับ a=1 เรามี ฟังก์ชันเชิงเส้นย=x
คุณสมบัติของฟังก์ชันยกกำลังที่มีเลขชี้กำลังบวกเป็นเลขคี่
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังบวกคู่
ลองพิจารณาฟังก์ชันยกกำลังที่มีเลขชี้กำลังบวกคู่ นั่นคือ สำหรับ a = 2,4,6,....
ตัวอย่างเช่น เราให้กราฟของฟังก์ชันกำลัง - เส้นสีดำ - เส้นสีน้ำเงิน - เส้นสีแดง สำหรับ a=2 เรามีฟังก์ชันกำลังสอง ซึ่งก็คือกราฟ พาราโบลากำลังสอง.
คุณสมบัติของฟังก์ชันยกกำลังที่มีเลขชี้กำลังบวกเป็นคู่
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังลบคี่
ดูกราฟของฟังก์ชันกำลังสำหรับค่าลบคี่ของเลขชี้กำลัง นั่นคือสำหรับ a = -1, -3, -5,....
รูปนี้แสดงกราฟของฟังก์ชันกำลังตามตัวอย่าง - เส้นสีดำ - เส้นสีน้ำเงิน - เส้นสีแดง - เส้นสีเขียว สำหรับ a=-1 เรามี สัดส่วนผกผันซึ่งเป็นกราฟของใคร ไฮเปอร์โบลา.
คุณสมบัติของฟังก์ชันยกกำลังที่มีเลขชี้กำลังเป็นลบคี่
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังเป็นลบคู่
มาดูฟังก์ชันยกกำลังสำหรับ a=-2,-4,-6,….
รูปนี้แสดงกราฟของฟังก์ชันกำลัง – เส้นสีดำ – เส้นสีน้ำเงิน – เส้นสีแดง
คุณสมบัติของฟังก์ชันยกกำลังที่มีเลขชี้กำลังเป็นลบคู่
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังที่เป็นตรรกยะหรืออตรรกยะซึ่งมีค่ามากกว่าศูนย์และน้อยกว่า 1
ใส่ใจ!ถ้า a เป็นเศษส่วนบวกที่มีตัวส่วนเป็นคี่ ผู้เขียนบางคนถือว่าโดเมนของคำจำกัดความของฟังก์ชันยกกำลังเป็นช่วง มีการกำหนดว่าเลขชี้กำลัง a เป็นเศษส่วนที่ลดไม่ได้ ตอนนี้ผู้เขียนหนังสือเรียนหลายเล่มเกี่ยวกับพีชคณิตและหลักการวิเคราะห์ไม่ได้กำหนดฟังก์ชันกำลังด้วยเลขชี้กำลังในรูปแบบของเศษส่วนที่มีตัวส่วนคี่สำหรับค่าลบของอาร์กิวเมนต์ เราจะยึดถือมุมมองนี้อย่างแม่นยำ กล่าวคือ เราจะถือว่าเซตนี้เป็นโดเมนของคำจำกัดความของฟังก์ชันยกกำลังที่มีเลขชี้กำลังบวกแบบเศษส่วน เราขอแนะนำให้นักเรียนค้นหาความคิดเห็นของครูเกี่ยวกับประเด็นที่ละเอียดอ่อนนี้เพื่อหลีกเลี่ยงความขัดแย้ง
ให้เราพิจารณาฟังก์ชันกำลังด้วยเลขชี้กำลังที่เป็นตรรกยะหรือไม่ลงตัว a และ
ให้เรานำเสนอกราฟของฟังก์ชันยกกำลังสำหรับ a=11/12 (เส้นสีดำ), a=5/7 (เส้นสีแดง), (เส้นสีน้ำเงิน), a=2/5 (เส้นสีเขียว)
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังที่เป็นตรรกยะหรืออตรรกยะที่ไม่ใช่จำนวนเต็มมากกว่า 1
ให้เราพิจารณาฟังก์ชันยกกำลังที่มีเลขชี้กำลังที่เป็นตรรกยะหรืออตรรกยะที่ไม่ใช่จำนวนเต็ม a และ
ให้เรานำเสนอกราฟของฟังก์ชันกำลังที่กำหนดโดยสูตร 
(เส้นสีดำ สีแดง สีน้ำเงิน และสีเขียว ตามลำดับ)
สำหรับค่าอื่นของเลขชี้กำลัง a กราฟของฟังก์ชันจะมีลักษณะคล้ายกัน
คุณสมบัติของฟังก์ชันกำลังที่
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังจริงที่มากกว่าลบหนึ่งและน้อยกว่าศูนย์
ใส่ใจ!ถ้า a เป็นเศษส่วนลบที่มีตัวส่วนเป็นคี่ ผู้เขียนบางคนถือว่าโดเมนของคำจำกัดความของฟังก์ชันยกกำลังเป็นช่วง 
- มีการกำหนดว่าเลขชี้กำลัง a เป็นเศษส่วนที่ลดไม่ได้ ตอนนี้ผู้เขียนหนังสือเรียนหลายเล่มเกี่ยวกับพีชคณิตและหลักการวิเคราะห์ไม่ได้กำหนดฟังก์ชันกำลังด้วยเลขชี้กำลังในรูปแบบของเศษส่วนที่มีตัวส่วนคี่สำหรับค่าลบของอาร์กิวเมนต์ เราจะยึดถือมุมมองนี้อย่างแม่นยำ กล่าวคือ เราจะพิจารณาโดเมนของคำจำกัดความของฟังก์ชันยกกำลังที่มีเลขชี้กำลังลบที่เป็นเศษส่วนให้เป็นเซต ตามลำดับ เราขอแนะนำให้นักเรียนค้นหาความคิดเห็นของครูเกี่ยวกับประเด็นที่ละเอียดอ่อนนี้เพื่อหลีกเลี่ยงความขัดแย้ง
มาดูฟังก์ชันกำลังกันดีกว่า
เพื่อให้มีความคิดที่ดีเกี่ยวกับรูปแบบของกราฟของฟังก์ชันกำลังสำหรับ เราจะยกตัวอย่างกราฟของฟังก์ชัน 
(เส้นโค้งสีดำ สีแดง สีน้ำเงิน และสีเขียว ตามลำดับ)
คุณสมบัติของฟังก์ชันยกกำลังที่มีเลขชี้กำลัง a,
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังจริงที่ไม่ใช่จำนวนเต็มซึ่งมีค่าน้อยกว่าลบหนึ่ง
ให้เรายกตัวอย่างกราฟของฟังก์ชันกำลังสำหรับ 
โดยมีเส้นสีดำ แดง น้ำเงิน และเขียว ตามลำดับ
คุณสมบัติของฟังก์ชันยกกำลังที่มีเลขชี้กำลังลบที่ไม่ใช่จำนวนเต็มน้อยกว่าลบหนึ่ง
เมื่อ a = 0 เรามีฟังก์ชัน - นี่คือเส้นตรงที่ไม่รวมจุด (0;1) (มีการตกลงกันว่าจะไม่ให้ความสำคัญใด ๆ กับนิพจน์ 0 0)
ฟังก์ชันเลขชี้กำลัง
ฟังก์ชันพื้นฐานหลักอย่างหนึ่งคือฟังก์ชันเลขชี้กำลัง
กราฟของฟังก์ชันเลขชี้กำลัง โดยที่ และ มีรูปแบบที่แตกต่างกัน ขึ้นอยู่กับค่าของฐาน a ลองคิดดูสิ
ขั้นแรก ให้พิจารณากรณีที่ฐานของฟังก์ชันเลขชี้กำลังรับค่าจากศูนย์ถึงหนึ่ง นั่นคือ
ตามตัวอย่าง เรานำเสนอกราฟของฟังก์ชันเลขชี้กำลังสำหรับ a = 1/2 – เส้นสีน้ำเงิน, a = 5/6 – เส้นสีแดง กราฟของฟังก์ชันเลขชี้กำลังมีลักษณะคล้ายกันสำหรับค่าอื่นของฐานจากช่วงเวลา
คุณสมบัติของฟังก์ชันเลขชี้กำลังที่มีฐานน้อยกว่าหนึ่ง
ให้เราไปยังกรณีที่ฐานของฟังก์ชันเลขชี้กำลังมีค่ามากกว่าหนึ่งนั่นคือ
เพื่อเป็นตัวอย่าง เราจะนำเสนอกราฟของฟังก์ชันเลขชี้กำลัง - เส้นสีน้ำเงินและ - เส้นสีแดง สำหรับค่าอื่นของฐานที่มากกว่าหนึ่ง กราฟของฟังก์ชันเลขชี้กำลังจะมีลักษณะคล้ายกัน
คุณสมบัติของฟังก์ชันเลขชี้กำลังที่มีฐานมากกว่าหนึ่ง
ฟังก์ชันลอการิทึม
ฟังก์ชันพื้นฐานพื้นฐานถัดไปคือฟังก์ชันลอการิทึม โดยที่ , . ฟังก์ชันลอการิทึมถูกกำหนดไว้สำหรับค่าบวกของอาร์กิวเมนต์เท่านั้นนั่นคือสำหรับ
กราฟของฟังก์ชันลอการิทึมมีรูปแบบที่แตกต่างกัน ขึ้นอยู่กับค่าของฐาน a
การรักษาความเป็นส่วนตัวของคุณเป็นสิ่งสำคัญสำหรับเรา ด้วยเหตุนี้ เราจึงได้พัฒนานโยบายความเป็นส่วนตัวที่อธิบายถึงวิธีที่เราใช้และจัดเก็บข้อมูลของคุณ โปรดตรวจสอบหลักปฏิบัติด้านความเป็นส่วนตัวของเราและแจ้งให้เราทราบหากคุณมีคำถามใดๆ
การรวบรวมและการใช้ข้อมูลส่วนบุคคล
ข้อมูลส่วนบุคคลหมายถึงข้อมูลที่สามารถใช้เพื่อระบุหรือติดต่อบุคคลใดบุคคลหนึ่งโดยเฉพาะ
คุณอาจถูกขอให้ให้ข้อมูลส่วนบุคคลของคุณได้ตลอดเวลาเมื่อคุณติดต่อเรา
ด้านล่างนี้คือตัวอย่างบางส่วนของประเภทของข้อมูลส่วนบุคคลที่เราอาจรวบรวมและวิธีที่เราอาจใช้ข้อมูลดังกล่าว
เราเก็บรวบรวมข้อมูลส่วนบุคคลอะไรบ้าง:
- เมื่อคุณส่งใบสมัครบนเว็บไซต์ เราอาจรวบรวมข้อมูลต่าง ๆ รวมถึงชื่อ หมายเลขโทรศัพท์ ที่อยู่อีเมลของคุณ ฯลฯ
เราใช้ข้อมูลส่วนบุคคลของคุณอย่างไร:
- ข้อมูลส่วนบุคคลที่เรารวบรวมช่วยให้เราสามารถติดต่อคุณเพื่อรับข้อเสนอ โปรโมชั่น และกิจกรรมอื่น ๆ และกิจกรรมที่กำลังจะเกิดขึ้น
- ในบางครั้ง เราอาจใช้ข้อมูลส่วนบุคคลของคุณเพื่อส่งประกาศและการสื่อสารที่สำคัญ
- เรายังอาจใช้ข้อมูลส่วนบุคคลเพื่อวัตถุประสงค์ภายใน เช่น การดำเนินการตรวจสอบ การวิเคราะห์ข้อมูล และการวิจัยต่างๆ เพื่อปรับปรุงบริการที่เรามีให้และให้คำแนะนำเกี่ยวกับบริการของเราแก่คุณ
- หากคุณเข้าร่วมการจับรางวัล การประกวด หรือการส่งเสริมการขายที่คล้ายกัน เราอาจใช้ข้อมูลที่คุณให้ไว้เพื่อจัดการโปรแกรมดังกล่าว
การเปิดเผยข้อมูลแก่บุคคลที่สาม
เราไม่เปิดเผยข้อมูลที่ได้รับจากคุณต่อบุคคลที่สาม
ข้อยกเว้น:
- หากจำเป็น - ตามกฎหมาย ขั้นตอนการพิจารณาคดี ในการดำเนินการทางกฎหมาย และ/หรือตามคำขอสาธารณะหรือคำขอจากหน่วยงานของรัฐในสหพันธรัฐรัสเซีย - ให้เปิดเผยข้อมูลส่วนบุคคลของคุณ เรายังอาจเปิดเผยข้อมูลเกี่ยวกับคุณหากเราพิจารณาว่าการเปิดเผยดังกล่าวมีความจำเป็นหรือเหมาะสมเพื่อความปลอดภัย การบังคับใช้กฎหมาย หรือวัตถุประสงค์ที่สำคัญสาธารณะอื่น ๆ
- ในกรณีของการปรับโครงสร้างองค์กร การควบรวมกิจการ หรือการขาย เราอาจถ่ายโอนข้อมูลส่วนบุคคลที่เรารวบรวมไปยังบุคคลที่สามที่รับช่วงต่อที่เกี่ยวข้อง
การคุ้มครองข้อมูลส่วนบุคคล
เราใช้ความระมัดระวัง - รวมถึงด้านการบริหาร ด้านเทคนิค และทางกายภาพ - เพื่อปกป้องข้อมูลส่วนบุคคลของคุณจากการสูญหาย การโจรกรรม และการใช้งานในทางที่ผิด รวมถึงการเข้าถึง การเปิดเผย การเปลี่ยนแปลง และการทำลายโดยไม่ได้รับอนุญาต
การเคารพความเป็นส่วนตัวของคุณในระดับบริษัท
เพื่อให้มั่นใจว่าข้อมูลส่วนบุคคลของคุณปลอดภัย เราจะสื่อสารมาตรฐานความเป็นส่วนตัวและความปลอดภัยให้กับพนักงานของเราและบังคับใช้หลักปฏิบัติด้านความเป็นส่วนตัวอย่างเคร่งครัด
สำคัญ!
ฟังก์ชันที่อยู่ในรูป “y = kx + b” เรียกว่าฟังก์ชันเชิงเส้น
เรียกตัวประกอบตัวอักษร "k" และ "b" ค่าสัมประสิทธิ์ตัวเลข.
แทนที่จะเป็น "k" และ "b" อาจเป็นตัวเลขใดก็ได้ (บวก ลบ หรือเศษส่วน)
กล่าวอีกนัยหนึ่ง เราสามารถพูดได้ว่า “y = kx + b” เป็นตระกูลของฟังก์ชันที่เป็นไปได้ทั้งหมด โดยที่แทนที่จะเป็น “k” และ “b” กลับกลายเป็นตัวเลข
ตัวอย่างฟังก์ชัน เช่น “y = kx + b”
- y = 5x + 3
- y = −x + 1
- y = x − 2
เค = 2 3 ข = −2 y = 0.5x เค = 0.5 ข = 0 ให้ความสนใจเป็นพิเศษกับฟังก์ชัน "y = 0.5x" ในตาราง พวกเขามักจะทำผิดพลาดในการหาค่าสัมประสิทธิ์ตัวเลข "b"
เมื่อพิจารณาฟังก์ชัน “y = 0.5x” การบอกว่าไม่มีสัมประสิทธิ์ตัวเลข “b” ในฟังก์ชันไม่ถูกต้อง
ค่าสัมประสิทธิ์ตัวเลข "b" จะแสดงอยู่ในฟังก์ชันเช่น "y = kx + b" เสมอ
ในฟังก์ชัน “y = 0.5x” ค่าสัมประสิทธิ์ตัวเลข “b” จะเป็นศูนย์
วิธีสร้างกราฟฟังก์ชันเชิงเส้น"y = kx + b"
จดจำ!.
กราฟของฟังก์ชันเชิงเส้น “y = kx + b” เป็นเส้นตรง เนื่องจากกราฟของฟังก์ชัน “y = kx + b” เป็นเส้นตรง จึงเรียกใช้ฟังก์ชันนี้.
ฟังก์ชันเชิงเส้น
จากเรขาคณิต ให้เรานึกถึงสัจพจน์ (ข้อความที่ไม่ต้องการการพิสูจน์) ที่ว่าผ่านจุดสองจุดใดๆ คุณสามารถวาดเส้นตรงและยิ่งไปกว่านั้นมีเพียงจุดเดียวเท่านั้น
ตามสัจพจน์ข้างต้น เป็นไปตามนั้นเพื่อพล็อตฟังก์ชันของแบบฟอร์ม“y = kx + b” เราจะหาเพียงสองจุดก็เพียงพอแล้ว ตัวอย่างเช่นมาสร้างกราฟของฟังก์ชันกันดีกว่า
"y = −2x + 1"
สำคัญ!
มาหาค่าของฟังก์ชัน "y" สำหรับค่าใดก็ได้สองค่า "x"
ให้เราแทนที่ตัวเลข "0" และ "1" แทน "x"
เมื่อเลือกค่าตัวเลขที่กำหนดเองแทน "x" ควรใช้ตัวเลข "0" และ "1"
การคำนวณตัวเลขเหล่านี้เป็นเรื่องง่าย
ค่าผลลัพธ์ "x" และ "y" คือพิกัดของจุดบนกราฟฟังก์ชัน
ลองเขียนพิกัดที่ได้รับของจุด “y = −2x + 1” ลงในตาราง
ให้เราทำเครื่องหมายจุดที่ได้รับบนระบบพิกัดทีนี้ลองวาดเส้นตรงผ่านจุดที่ทำเครื่องหมายไว้ เส้นนี้จะเป็นกราฟของฟังก์ชัน “y = −2x + 1”
วิธีแก้ปัญหาเมื่อ
- ฟังก์ชันเชิงเส้น “y = kx + b”
- ลองพิจารณาปัญหา
สร้างกราฟฟังก์ชัน “y = 2x + 3” ค้นหาตามกราฟ:
ค่า "y" ตรงกับค่า "x" เท่ากับ −1; 2; 3; 5 ;
ค่าของ "x" ถ้าค่าของ "y" คือ 1; 4; 0; −1.
ก่อนอื่น เรามาพลอตฟังก์ชัน “y = 2x + 3” กันก่อน
เราใช้กฎที่เราเหนือกว่า
หากต้องการสร้างกราฟฟังก์ชัน "y = 2x + 3" ก็เพียงพอที่จะหาเพียงสองจุดเท่านั้น
ลองเลือกค่าตัวเลขสองค่าสำหรับ "x" เพื่อความสะดวกในการคำนวณเราเลือกตัวเลข "0" และ "1"
คุณต้องค้นหาค่า "y" ที่สอดคล้องกับค่า "x"
ซึ่งเท่ากับ −1; 2; 3; 5.- วัว"ถึงศูนย์ (x = 0) ;
- แทนที่ศูนย์สำหรับ "x" ในสูตรฟังก์ชันและค้นหาค่า "y"
- ออย".
แทนที่จะเป็น “x” ในสูตรของฟังก์ชัน “y = −1.5x + 3” ให้แทนที่เลขศูนย์แทน
Y(0) = −1.5 0 + 3 = 3
(0; 3) - พิกัดของจุดตัดของกราฟของฟังก์ชัน "y = −1.5x + 3" กับแกน "Oy""y = kx + b"
เพื่อค้นหาพิกัดของจุดตัดของกราฟของฟังก์ชัน
มีแกน” วัว"(แกน x) คุณต้องการ:- เทียบพิกัดของจุดตามแกน "" ออย"ถึงศูนย์ (y = 0) ;
- แทนที่ศูนย์แทน "y" ในสูตรฟังก์ชันและค้นหาค่าของ "x"
- เขียนพิกัดที่ได้รับของจุดตัดกับแกน " ออย".
แทนที่จะใช้ “y” ในสูตรของฟังก์ชัน “y = −1.5x + 3” ให้แทนที่เลขศูนย์แทน
0 = −1.5x + 3
1.5x = 3 | :(1.5)
x = 3: 1.5
x = 2
(2; 0) - พิกัดของจุดตัดของกราฟของฟังก์ชัน "y = −1.5x + 3" ด้วยแกน "Ox"เพื่อให้ง่ายต่อการจดจำว่าพิกัดใดของจุดที่ควรเท่ากับศูนย์ ให้จำ "กฎของจุดตรงข้าม"
สำคัญ!
หากคุณต้องการหาพิกัดของจุดตัดของกราฟกับแกน " วัว"จากนั้นเราถือว่า "y" เป็นศูนย์
และในทางกลับกัน หากคุณต้องการค้นหาพิกัดของจุดตัดของกราฟด้วยแกน "" ออย"จากนั้นเราถือว่า "x" เป็นศูนย์
มหาวิทยาลัยวิจัยแห่งชาติ
ภาควิชาธรณีวิทยาประยุกต์
บทคัดย่อเกี่ยวกับคณิตศาสตร์ชั้นสูง
ในหัวข้อ: “ฟังก์ชันพื้นฐานเบื้องต้น
คุณสมบัติและกราฟของพวกเขา"
สมบูรณ์:
ตรวจสอบแล้ว:
ครู
คำนิยาม. ฟังก์ชันที่กำหนดโดยสูตร y=a x (โดยที่ a>0, a≠1) เรียกว่าฟังก์ชันเลขชี้กำลังที่มีฐาน a
ให้เรากำหนดคุณสมบัติหลักของฟังก์ชันเลขชี้กำลัง:
1. โดเมนของคำจำกัดความคือเซต (R) ของจำนวนจริงทั้งหมด
2. พิสัย - เซต (R+) ของจำนวนจริงบวกทั้งหมด
3. สำหรับ a > 1 ฟังก์ชันจะเพิ่มขึ้นตามเส้นจำนวนทั้งหมด เวลา 0<а<1 функция убывает.
4. เป็นฟังก์ชันรูปแบบทั่วไป
, ในช่วงเวลา xО [-3;3]
, ในช่วงเวลา xО [-3;3] ฟังก์ชันที่อยู่ในรูปแบบ y(x)=x n โดยที่ n คือตัวเลข ОR เรียกว่าฟังก์ชันยกกำลัง จำนวน n สามารถใช้กับค่าที่แตกต่างกันได้ ทั้งจำนวนเต็มและเศษส่วน ทั้งเลขคู่และคี่ ฟังก์ชันกำลังจะมีรูปแบบที่แตกต่างกันขึ้นอยู่กับสิ่งนี้ ลองพิจารณากรณีพิเศษที่เป็นฟังก์ชันกำลังและสะท้อนถึงคุณสมบัติพื้นฐานของเส้นโค้งประเภทนี้ตามลำดับต่อไปนี้: ฟังก์ชันกำลัง y=x² (ฟังก์ชันที่มีเลขชี้กำลังเลขคู่ - พาราโบลา) ฟังก์ชันกำลัง y=x³ (ฟังก์ชันที่มีเลขชี้กำลังคี่ - ลูกบาศก์พาราโบลา) และฟังก์ชัน y=√x (x ยกกำลัง ½) (ฟังก์ชันที่มีเลขชี้กำลังเศษส่วน) ฟังก์ชันที่มีเลขชี้กำลังจำนวนเต็มลบ (ไฮเปอร์โบลา)
ฟังก์ชั่นพลังงาน ย=x²
1. D(x)=R – ฟังก์ชันถูกกำหนดบนแกนตัวเลขทั้งหมด
2. E(y)= และเพิ่มขึ้นตามช่วงเวลา
ฟังก์ชั่นพลังงาน y=x³
1. กราฟของฟังก์ชัน y=x³ เรียกว่าลูกบาศก์พาราโบลา ฟังก์ชันกำลัง y=x³ มีคุณสมบัติดังต่อไปนี้:
2. D(x)=R – ฟังก์ชันถูกกำหนดบนแกนตัวเลขทั้งหมด
3. E(y)=(-∞;∞) – ฟังก์ชันรับค่าทั้งหมดในโดเมนของคำจำกัดความ
4. เมื่อ x=0 y=0 – ฟังก์ชันจะผ่านจุดกำเนิดของพิกัด O(0;0)
5. ฟังก์ชันจะเพิ่มขึ้นทั่วทั้งขอบเขตคำจำกัดความ
6. ฟังก์ชันเป็นเลขคี่ (สมมาตรเกี่ยวกับจุดกำเนิด)
, ในช่วงเวลา xО [-3;3] ขึ้นอยู่กับปัจจัยตัวเลขที่อยู่ด้านหน้า x³ ฟังก์ชันสามารถชัน/คงที่ และเพิ่ม/ลดได้
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังจำนวนเต็มลบ:
ถ้าเลขชี้กำลัง n เป็นเลขคี่ กราฟของฟังก์ชันยกกำลังจะเรียกว่าไฮเปอร์โบลา ฟังก์ชันยกกำลังที่มีเลขชี้กำลังลบจำนวนเต็มมีคุณสมบัติดังต่อไปนี้:
1. D(x)=(-∞;0)U(0;∞) สำหรับ n ใดๆ;
2. E(y)=(-∞;0)U(0;∞) ถ้า n เป็นเลขคี่ E(y)=(0;∞) ถ้า n เป็นเลขคู่
3. ฟังก์ชันจะลดลงทั่วทั้งโดเมนของคำจำกัดความ ถ้า n เป็นเลขคี่ ฟังก์ชันจะเพิ่มขึ้นในช่วงเวลา (-∞;0) และลดลงในช่วงเวลา (0;∞) ถ้า n เป็นเลขคู่
4. ฟังก์ชันจะเป็นเลขคี่ (สมมาตรเกี่ยวกับจุดกำเนิด) ถ้า n เป็นเลขคี่ ฟังก์ชันจะเป็นแม้ว่า n จะเป็นเลขคู่ก็ตาม
5. ฟังก์ชันจะส่งผ่านจุด (1;1) และ (-1;-1) ถ้า n เป็นเลขคี่ และผ่านจุด (1;1) และ (-1;1) ถ้า n เป็นเลขคู่
, ในช่วงเวลา xО [-3;3] ฟังก์ชันยกกำลังพร้อมเลขชี้กำลังเศษส่วน
ฟังก์ชันยกกำลังที่มีเลขชี้กำลังเศษส่วน (รูปภาพ) มีกราฟของฟังก์ชันดังแสดงในรูป ฟังก์ชันยกกำลังที่มีเลขชี้กำลังเศษส่วนมีคุณสมบัติดังต่อไปนี้: (รูปภาพ)
1. D(x) ОR ถ้า n เป็นเลขคี่ และ D(x)= 
ในช่วงเวลา xO 
, ในช่วงเวลา xО [-3;3]
ฟังก์ชันลอการิทึม y = log a x มีคุณสมบัติดังต่อไปนี้:
1. โดเมนของคำจำกัดความ D(x)О (0; + ∞)
2. ช่วงค่า E(y) О (- ∞; + ∞)
3. ฟังก์ชันไม่เป็นคู่หรือคี่ (ในรูปแบบทั่วไป)
4. ฟังก์ชั่นเพิ่มขึ้นในช่วงเวลา (0; + ∞) สำหรับ a > 1 ลดลง (0; + ∞) สำหรับ 0< а < 1.
กราฟของฟังก์ชัน y = log a x สามารถหาได้จากกราฟของฟังก์ชัน y = a x โดยใช้การแปลงสมมาตรรอบเส้นตรง y = x รูปที่ 9 แสดงกราฟของฟังก์ชันลอการิทึมสำหรับ a > 1 และรูปที่ 10 สำหรับ 0< a < 1.
- ในช่วงเวลาxО 
- ในช่วงเวลาxО ฟังก์ชัน y = sin x, y = cos x, y = tan x, y = ctg x เรียกว่าฟังก์ชันตรีโกณมิติ
ฟังก์ชัน y = sin x, y = tan x, y = ctg x เป็นเลขคี่ และฟังก์ชัน y = cos x เป็นเลขคู่
ฟังก์ชัน y = บาป(x)
1. โดเมนของคำจำกัดความ D(x) ОR
2. ช่วงของค่า E(y) О [ - 1; 1].
3. ฟังก์ชั่นเป็นระยะ คาบหลักคือ 2π
4. ฟังก์ชันเป็นเลขคี่
5. ฟังก์ชันจะเพิ่มขึ้นตามช่วงเวลา [ -π/2 + 2πn; π/2 + 2πn] และลดลงตามช่วง [π/2 + 2πn; 3π/2 + 2πn], n О Z
กราฟของฟังก์ชัน y = sin (x) แสดงในรูปที่ 11